Probing of plasma singularities and Lampa-Penrose-Terrell effect
Note: This is a copy of press-release of the paper by T. Zh. Esirkepov et al., Phys. Plasmas 27, 052103 (2020) which I co-authored.
A team of researchers from Kansai Photon Science Institute (Japan), ELI Beamlines (Czech Rep.), and Central Laser Facility (UK) proposed a method for observing the Lampa-Penrose-Terrell effect via optical probing of relativistic plasma singularities, according to a paper recently published in Physics of Plasmas.
Plasma singularities
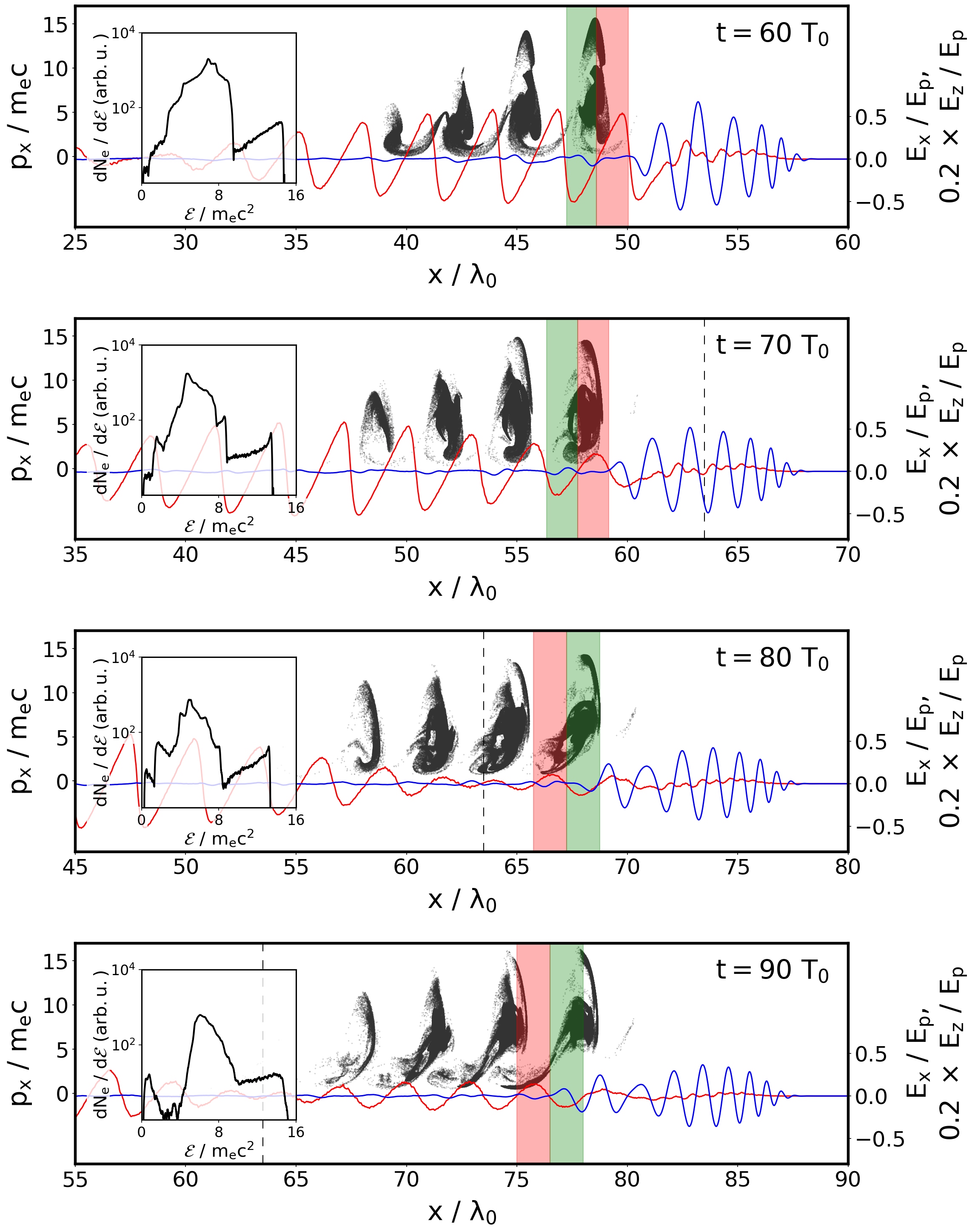
The authors show that imaging of relativistically moving singularities in plasma density is feasible using an ultrafast optical probe with the schlieren technique. Singularities are ubiquitous in relativistic plasma driven by an intense laser; they appear due to the breaking of plasma waves, which is a manifestation of a strongly nonlinear laser-plasma interaction.
The density singularities play an important role in many envisioned plasma-based applications, such as production of high-frequency electromagnetic radiation or accelerated electrons. An ability to detect these singularities in experiments would be therefore very advantageous. However, their direct observation is challenging due to their extreme sharpness (tens of nanometers), relativistic velocity, and transient non-local nature.
Schlieren imaging
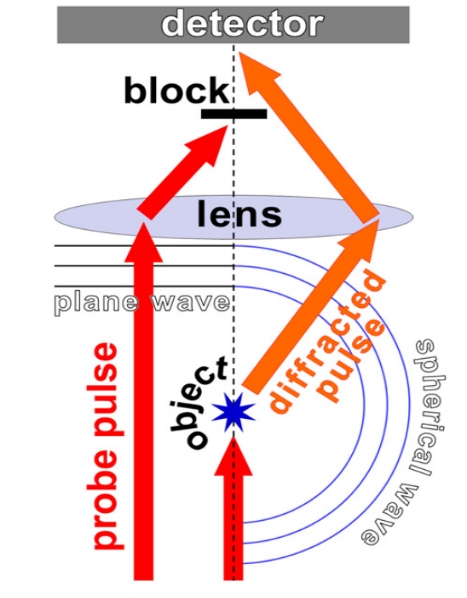
Schlieren imaging relies on the fact that light rays are bent whenever they encounter changes in density of a media. After the rays of the probe pass the medium, they can be therefore divided into two groups: those that interacted with the density singularities and those that did not. The latter group of rays remains parallel, so it can be brought to a single sharp focus by a lens and filtered out. On the other hand, the rays that interacted with the singularities are deflected and directed on a detector where they form a two-dimensional projection image (see Figure 1).
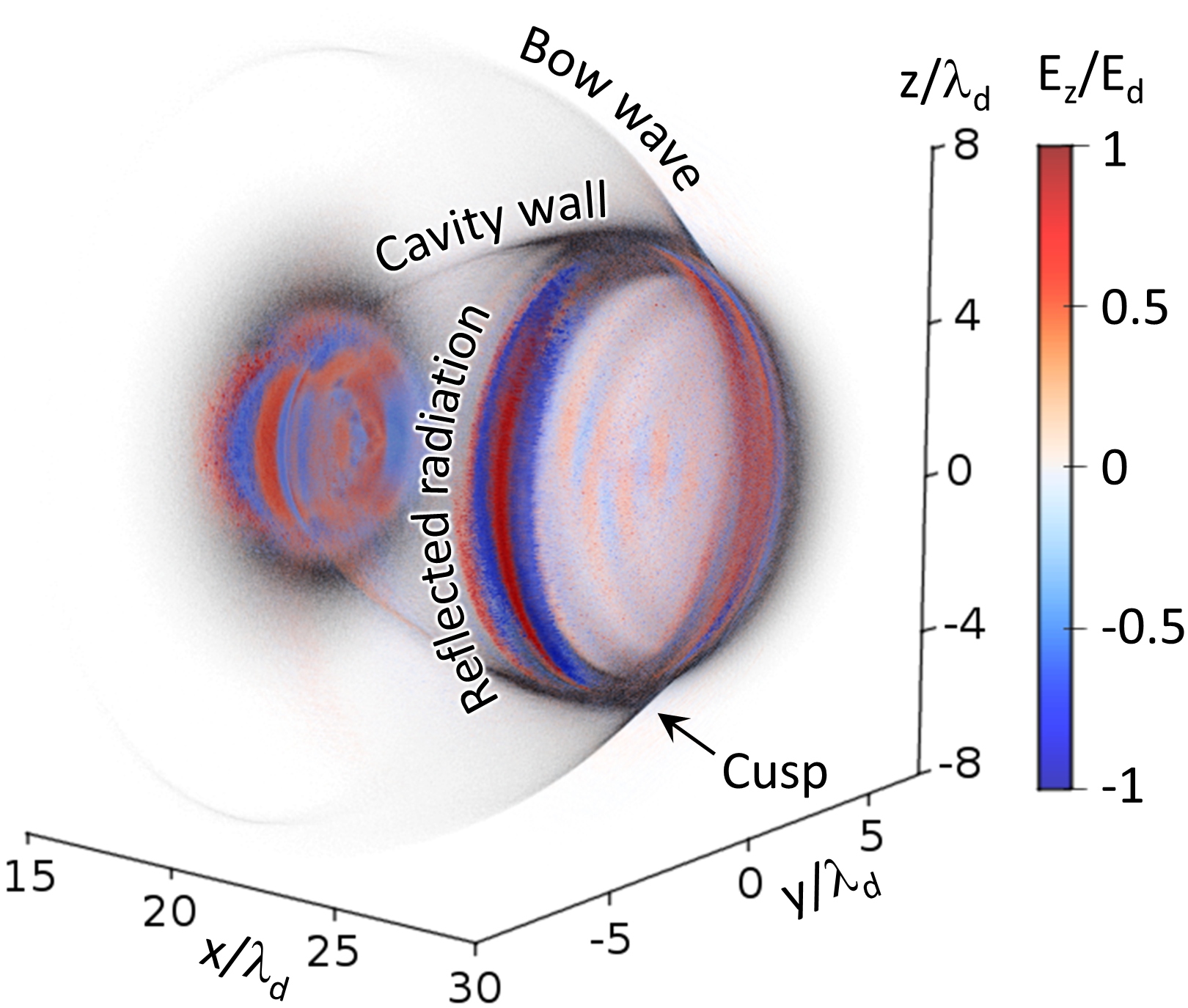
The authors demonstrate their method on one particularly interesting example of singularity: a high-density electron ring that is (under proper conditions) formed around an intense laser pulse in plasma. Their findings are supported by analytical estimates and computer simulations. They point out that the probe pulse has to be very short (several optical cycles) in order to discernible the shape of the singularity. However, such probes are already available at modern laser facilities.
Lampa-Penorse-Terrell effect
The authors note that the image of the constellation of density singularities in plasma will be such as if the singularities were slightly rotated with respect to each other – this corresponds to the Lampa-Penrose-Terrell effect (see Figure 2).

As widely accepted, Einstein’s special relativity explains the object contraction in length when it travels near the speed of light. But after Lampa, Penrose, and Terrell we know if one could take a photograph of such an object, it would not look shorter at all – it would seem to have been rotated because the object has been at different locations when different parts of it have emitted the light seen in the photograph.
Tip: You may find a pre-print of this paper on arXiv.
How to cite
T. Zh. Esirkepov, J. Mu, Y. Gu, T. M. Jeong, P. Valenta, O. Klimo, J. K. Koga, M. Kando, D. Neely, G. Korn, S. V. Bulanov, and A. S. Pirozhkov, “Optical probing of relativistic plasma singularities”, Physics of Plasmas 27, 052103 (2020).
@article{doi:10.1063/5.0004525,
author = {Esirkepov,Timur Zh. and Mu,Jie and Gu,Yanjun and Jeong,Tae Moon and Valenta,Petr and Klimo,Ondrej and Koga,James K. and Kando,Masaki and Neely,David and Korn,Georg and Bulanov,Sergei V. and Pirozhkov,Alexander S. },
title = {Optical probing of relativistic plasma singularities},
journal = {Physics of Plasmas},
volume = {27},
number = {5},
pages = {052103},
year = {2020},
doi = {10.1063/5.0004525},
URL = { https://doi.org/10.1063/5.0004525},
eprint = {https://doi.org/10.1063/5.0004525}
}